An Interview with Sarah Voss

Holos: Forum for a New Worldview
Vol. 5, No. 2 (2009)
Sarah Voss is the author of What Number Is God? Metaphors, Metaphysics, Metamathematics, and the Nature of Things (SUNY Press, 1995) and Zero: Reflections about Nothing (Cross-Cultural Publications, 1999). She has also authored a book about her interim ministry entitled Voice to Voice, Heart to Heart (Skinner House Books, 1996), as well as a chapbook of poem-prayers, Out of Our Prayers, Hope. Various of her articles and essays are available on her website. In the course of her diverse life, Sarah Voss has been a mathematics professor, a Unitarian Universalist minister, and a mediator. She holds a Doctor of Ministry from the Meadville Lombard Theological School in Chicago.
The text below is a record of written correspondence between Thomas McFarlane and Sarah Voss during 2009. This document is copyright © 2009 by Sarah Voss and is published here with her kind permission.
[Note: As a convenience to readers, some names and technical terms in this document are linked to external web resources. These links, however, do not constitute an implicit or explicit endorsement of any information found on those external pages.]
Introduction
Tom McFarlane: Thank you for agreeing to this interview. I'm very glad to have this opportunity to learn more about your life and work because you have a very unique background as both a professor of mathematics and, later, as a Unitarian Universalist minister. Perhaps most importantly, though, you have worked to explore some fascinating connections between these two fields of knowledge, such as in your book What Number is God?
Before we get into these very interesting topics, however, I'd like to first ask if you would share with us some of your personal background. Perhaps you could start by telling us a bit about your upbringing, for example, where you grew up and what your childhood was like. Were you raised in any particular religious tradition?
Sarah Voss: Thanks for asking, Tom. I appreciate the opportunity to become a Holos interviewee. It's an honor to be asked. I'm happy to share a bit about my personal background—and most everything else, too.
I was raised on a dairy farm in the northeastern corner of Ohio. We lived about seven miles from Lake Erie, but visited it only rarely and in the summer, usually when my cousins from Kansas came for a visit and then never after early-August when the danger of getting polio seemed (according to my mother) to increase significantly. Mine was a pretty conventional rural upbringing—quite conservative as I look back on it, with 4-H every summer (sewing and showing my Guernsey heifer) and every Sunday the Congregational church (youth choir once a month and confirmation by the time I was eleven). I've just finished writing all about my upbringing (and more) in a book whose working title is Self-Making: Autopoiesis of Woman. It's my personal story, written with a mathematical underpinning. "Autopoiesis" is translated variously as self-emerging, self-forming, or self-making, so the subtitle is redundant. I suppose that's another rule I've broken.
Tom: What drew you to the study of mathematics in college? And, later, what motivated you to seek a career in academia as a mathematician? Did you have an interest in religion during this period of your life? Did you have a sense of the connection between the two back then?
Sarah: I was good in math. I was good in English, too. I was also insecure about a ton of things, especially finding a husband—which was the golden goal of every girl I knew back then. In college I majored in math because 1) I qualified to participate in a unique undergraduate honors program in mathematics and 2) I thought there'd be more opportunity to meet my future husband if I went into math. Not exactly the most admirable reasons, I admit, but I was young.
I always wanted to write, but mathematics kept finding me one way or another. Like the time after I'd quit teaching math to ninth-graders and never wanted to teach anything to anyone else ever again, and I applied for a position as a public relations director at a small community college in Maryland (my home at the time). I wrote a great cover letter which got me an interview, but the personnel department quickly scoped out my total lack of qualifications for the position I wanted and offered me a job teaching math instead. That sort of thing happened to me all of my life, the second twenty years of which (to address the last part of your question, Tom) I called myself an atheist. So, yes, I had a strong interest in religion during that period of time; it was just highly negative. Not the same thing at all as apathy. As for a connection between math and religion back then? Nada. Not a bit. Not that I could see, anyway. I never ventured out of Plato's cave back then.
Tom: Could you elaborate a bit about how you came to identify yourself as an atheist? When did that transition take place? Was there some specific dissatisfaction or negative experience that drove you away from religion?
Sarah: Perceptive questions, Tom. I think my atheism probably started when I was a teenager and was super-sensitive, super-critical, and super-insecure. As a young teen I also had a close-call with death which took me through a "life-review," but didn't seem to get me to that "light at the end of the tunnel" stage. Emotionally, I felt rejected and distrustful, both in my social and spiritual lives. Somehow I eventually translated that into a strong intellectual conviction that life was purely material. That conviction lasted into my late thirties, and was not easily shattered even then.
Tom: During your time as a professional mathematician, what was the relationship for you between mathematics and religion? How did your interest in relating these two areas of knowledge emerge for you?
Sarah: At first there wasn't any connection for me. At that time I considered "religion" a bad word, while mathematics represented something I could trust—like the rest of the scientific world. I had a strong desire to avoid what I considered the hypocrisy of the religious world, and I certainly didn't want to subject my young, impressionable children to it! My world didn't have a lot of hope in it then, and none that was non-material.
Then I had what I refer to (depending upon my audience and/or mood) as a mid-life crisis or the dark night of a mystic journey. That story is too long to tell here. Anyway, one day not long thereafter when I was mathematics program director at an all-women's Catholic college, I began to tell my five female calculus students how God was like the definite integral of calculus. I watched myself telling them this, and even I thought it was a little odd. Soon after that, however, I began to seriously investigate the relationship between mathematics and religion. It was a hard go. Most of my contemporaries didn't think there was a relationship between mathematics and religion.
Tom: Although you've indicated it is a long story, could you say something more about your transformation from an atheist to a mystic? Did mathematics play a part in your mystical transformation during this period?
Sarah: I go into more detail about this in Self-Making. Let me just say here that an ex-priest was the catalyst for my transformation and that a messed-up surgery left me withering in enough pain that for a short period I'd have welcomed any form of relief, even death. I think that my inner willingness at that point to give up my "material" life helped prepare me psychologically for the major spiritual change which would follow in the next few years. Mathematics definitely accompanied and supported the intellectual part of this transformation, but it was not causal.
Tom: What prompted you to change your career from mathematics to ministry? What drew you to the Unitarian Universalist (UU) tradition?
Sarah: After my mystic conversion, I felt a strong call to the ministry. I pretty much felt compelled to try to become a minister. I don't think anyone should become a minister if they can possibly do anything else. When I was enmeshed in my "dark hour," I'd found Unitarian Universalism. On a liberal-to-conservative continuum of religions with Protestant origins, Unitarian Universalism was at the far left end, a bit more religiously-liberal than Congregationalism. It was a good fit for me in my aspiring search for truth. It still is. There is a great deal of freedom (and a less immediately obvious demand for responsibility) in UUism to pursue this search.
Tom: Did you begin your ministry with the idea to relate mathematics and religion, or did that emerge later? How has your work relating mathematics and religion developed over the years?
Sarah: When I went to seminary, I intentionally took mathematics with me. I knew I wanted to explore the relationship between math and religion more intensively, and I believed (more-or-less correctly) that I could do so through the UU faith tradition. I entered theological school with a profound desire to write my doctoral thesis on the topic. By this time I'd realized that mathematics, like poetry, was one of the languages historically used to try to communicate the mystic experience. Think of Abbot's Flatland, for example, where poor A. Square journeyed into Sphereland and was forever changed. I went to seminary wanting to find out more about how that language worked. I figured maybe then, by some gift of God's grace, I might find myself in a situation where I might actually be able to assist someone else in finding the hope I myself had found in and through mysticism.
As for how this work (relating mathematics and religion) developed over the years, the short answer is amazingly well. I was able to accomplish 51.388% of what I hoped to do. I'm kidding. I just like the sound of precision in 51.388%! Precision has been conspicuously absent in "how my work developed over the years." But, somewhere around "half of my expectations and endeavors were realized" is probably pretty descriptive. I've developed and taught an award-winning class about the relationship between math and religion. I've written extensively about the subject. I've offered workshops, lectures, and have even preached about it. Not long ago I accompanied a "science and religion" class from Rensselaer Polytechnic Institute as guest faculty on a two-week trip to Italy. I've also had some disappointments, such as a class on "moral" math which I was very excited about offering at my seminary but which didn't get enough students to "make," and a traveling museum display which I spent hours of time and vast amounts of energy developing but which I was never able to get funded, and an online journal which I sort of let slip away quietly into the zone of a personal website. There's just not been very much money—either to live on or to bring some of my ideas to fruition. But the inner rewards have been bountiful, and, probably, more to the point of your question. Over the years, I've enlarged the focus of my work to include not only matheology, but something I refer to as moral math, an umbrella term (not original to me—I think I first heard it from Sal Restivo of RPI) to include ways in which mathematics can help inform everything from conflict resolution to how we vote. I see this as a ripe arena for further exploration. The possibilities are exciting.
Tom: You once offered to the church you were serving five sermons based on different mathematical metaphors. What prompted you to give these sermons and what were the metaphors? How were these sermons received?
Sarah: Oh, goodness, I can't even remember which sermons those were, only that they were five of the early ones. What prompted me was that I'd discovered (in researching my thesis) that a major way in which the language of mathematics was historically used to expand our understandings of spirituality was through the use of what I call mathaphors—i.e., metaphors drawn from mathematics. Mathaphors, in other words, were hugely important to what I've called matheology. That's the main premise of my book What Number Is God? (which, not co-incidentally, started out life as my doctoral thesis). Was it surprising that I'd want to share mathaphors from the pulpit? Not to me. I wanted to share these ideas any way I could, just as any other (overzealous?) mystic might.
Mathaphors, however, have current as well as historical importance. Today's culture is largely caught up in the truths of science, which consistently uses mathematics as the primary language for both exploration and communication. To me, that means mathematics is also an exquisite candidate for contemporary spiritual exploration. Lewis Thomas, author of many books on science, medicine, language, and philosophy, once referred to mathematics as the universal language of the future. So, sure, I've "spoken" mathematics from the pulpit. How? Well, carefully. And not all the time, either. I remember early on in my professional ministry how I announced that I would be giving one of my "math" sermons on an up-coming Sunday. One person, whose math anxiety was extreme, stayed away altogether. For quite a while after that I gave the sermon first and then told them what it was!
Here are the names of some of my "math" sermons. 'Coming Out' of the Math Closet; The 'Strange Attractor' of Hope; Reflections about Nothing; Out of Statistics, Hope; Prayers that Count; Our Electronic Church; Gödel on Evil; Our Entangled Web (that one was a bust); God and Quantum Transitions; Computers and Consciousness; Towards a Cantorian Religion; How Fuzzy Logic Might Save Souls. That's probably half of them. I tried to interest a publisher in putting together a book of them, but, alas, without success. You need a lot of resilience to be a pioneer in this field!
Tom: Although it may sound surprising to modern ears, in your book you say that mathematics has been used throughout human history as a connecting device between metaphysics, theology, and religion. Who are some of the historical precursors to this perspective that mathematics has some relevance for religion? Do you have in mind Pythagoras? Nicholas of Cusa? Cantor? Others?
Sarah: Yes. Yes. Yes. Others include Plato, Galileo, Novalis, Jacobi, Kronecker.
Tom: In your book you write about how mathematics provides a metaphor for understanding metaphysics, and you describe a metaphor as a way of seeing. Could you elaborate on this idea a bit, and perhaps provide a simple example of what you mean? Do you think there is something special or fundamental about mathematics as a metaphor for viewing reality?
Sarah: Feminist theologian Sallie McFague once defined a metaphor as "seeing one thing as something else." We "see as." For example, we see God as Father, and we act accordingly. We see God as Mother, and our actions are likely to change somewhat to fit this alternative way of seeing. In this sense a metaphor is a way of seeing. Mathematics provides not just "a" metaphor for understanding metaphysics, but lots of them. Some offer better ways of seeing than others.
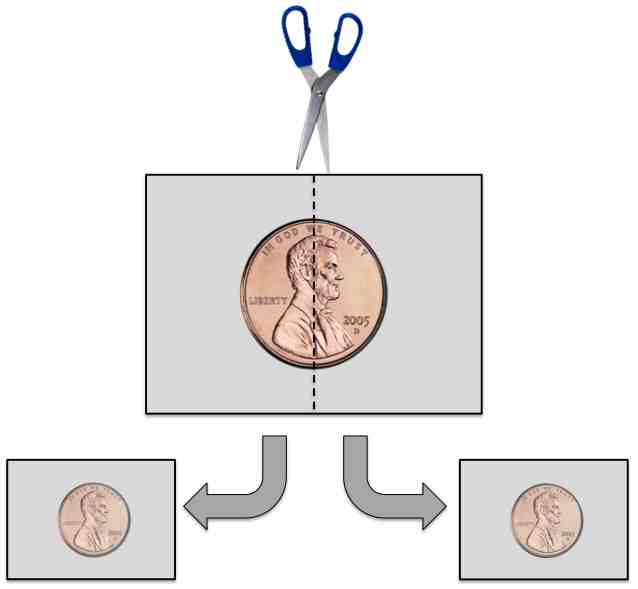
Take holography, for instance. In one math and religion class I taught, I invited a skilled physics professor to demonstrate the characteristics of holography—particularly, the surprising property that each part of a holographic image is in some sense equivalent to the whole. The professor arrived in our classroom equipped with an appropriate piece of "film" and all the other tools he needed to produce a holographic image. He then took a holographic "picture" of an ordinary penny. When he was done, he passed the film around so that all of the students could see for themselves what the image looked like. It looked just exactly like what all of us who have seen both a hologram and a penny might expect it to look like—something a little on the order of a "ghostly" one-cent coin. After everyone in the class had seen the image, the professor used a pair of scissors to snip the "picture" right down the middle, in effect splitting the penny into two parts. Everyone gaped in surprise after examining these two separate pieces of film because each one showed the penny in its entirety. Each part was equivalent to the whole.
The physics professor was demonstrating science, not mathematics, but the thing about holography is that the whole process was spelled out clearly in mathematics maybe twenty years or so before the technology (i.e., the laser) was invented to turn the theory into a material reality. The mathematics came first. Then came the technology to make images we could hold in our physical hands. Then, still later on, came the idea that we could use the notion of holography to see something else as if it were a hologram. David Bohm, Einstein's coworker, was probably the first to identify the metaphorical possibilities of holography. Bohm developed a model of reality that sees each part of energy and matter as a microcosm that enfolds the whole. Later Michael Talbot and Stanislav Grof (to cite two contemporary examples) used Bohm's ideas to create their own metaphysical versions of reality, each revealed, respectively, in their books, The Holographic Universe and The Holotropic Mind. The titles of those two books alone illustrate what I mean about how mathematics can be used as a metaphor for viewing reality.

Tom: Physicist Eugene Wigner once famously wrote about the "unreasonable effectiveness of mathematics in the physical sciences." What are your thoughts on this mystery? What explanation would you propose to understand how it is that mathematics works so well in physics?
Sarah: I am awed by this mystery. How would I propose to explain this wonder? I wouldn't. I just enjoy it. That's pretty much how I feel about the mystery of life, too. The best I can do is describe it, or at least the part of it I'm familiar with, and I'm apt to do that with mathaphors. In fact, that's what I just did in my book, Self-Making: Autopoiesis of Woman. I looked at my life as though it were an autopoietic process and used nine of the characteristics of this process to structure my story. I think chaos theorists, to name one potential audience, will be interested. If others are interested, too, then maybe it will find a publisher. (There is hope!)
Tom: In one place in your book you write that "nature is just mathematics that you can touch." [p.42] Could you elaborate on what you mean by this? It sounds similar to Galileo's view that the book of nature is written in mathematics but you seem to go further by saying that nature is not merely described by mathematics, but is mathematics.
Sarah: There does seem to be a mathematical structure undergirding nature. Is nature mathematics? I guess my answer is yes and no. Does a human need a human skeletal structure in order to be a human? Yes. Is a human its skeletal structure? No, not really. It's something like that, I think, between math and nature.
Tom: A series of quotations in your book [p.76] seem to suggest that the very existence of things is essentially mathematical. For example, Philolaus says that "All things have a number, and it is this fact which enables them to be known." Philo says number was "the basis of the design of the Creator" and "the number itself, rather than its concrete representation, is considered the ultimate reality." Dionysius the Areopagite wrote that "to the best of our ability, we use symbols appropriate to things Divine, and from these again we elevate ourselves, according to our degree, to the simple and unified truth of the spiritual visions." Can you explain in what sense numbers are built into the very nature of reality?
Sarah: This is tricky, Tom, and I'm not sure how well I can answer your question. I can tell you that it is possible to understand the very existence of things as essentially mathematical. That is one way of seeing. I think the quotes which you refer to on page 76 indicate that a variety of individuals throughout history seem to have engaged in that kind of perspective. It is not the only way. And even seeing "the very existence of things as essentially mathematical" is open to a variety of interpretations. In fact, the whole section of my book around page 76 refers to number symbolism, which is more popularly known as numerology. I confess I'm not much of a numerologist, although I can remember applying one such system to my own birth name and determining that I was an "8"—or something like that. I recall avidly reading what it meant to be an "8." It felt a lot like reading my horoscope: no matter what I read, it fit. Numerology can be fun. But true? The Enneagram is a more recent variation of numerology and I know some folks who put great stock in it. What the heck, Augustine put great stock in number symbolism, too. He thought it was a way to discover the "mysteries of God which are set down in Scripture." More recently, Michael Drosnin set forth a highly popular (and controversial) variation of Augustine's position in The Bible Code. It, also, was fun reading, but it's not exactly what really gets me going.
Tom: The quote above from Dionysius suggests that mathematics actually can be used for more than merely gaining intellectual understanding. He seems to suggest that mathematics can actually help to attain a mystical illumination. Kurt Gödel also seemed to hold this view. For example, Hao Wang from his book, Reflections On Kurt Gödel, p 196, writes "He [Gödel] also looked for (but failed to obtain) an epiphany (a revelation or sudden illumination) that would enable him to see the world in a different light. (In his conversations with me, he repeatedly said that Plato, Descartes, and Husserl all had such an experience.)" What are your thoughts on (or experiences with) mathematics as a way of mystical illumination?
Sarah: To the best of my knowledge, any efforts I've made to illuminate the mystical way for someone else haven't gone very far. I actually don't spend much effort trying to be a guiding light. It feels presumptuous and a little arrogant. I have sown lots of thought-seeds, though, and many of them are mathematical in nature. Who knows what will happen to those seeds in the future?
Mathematics, however, has played a fundamental role in the way I claim my own mystical insights. Math has provided ways for me to grasp things that I couldn't comprehend in any other fashion. One example (which I mentioned earlier) is the way the part can be equivalent to the whole; the mathematical theory of holography helped me accept this contradiction. Because I trust the mathematics, I am comfortable saying to myself that perhaps something similar is true in the mystic world. That is, my mathematical knowledge both supports and expands my mystic understanding that the divine in each of us is a microcosm of a much greater divine.
Tom: In theology there is the paradox that God is not merely the sum of everything but in some sense transcends everything and is more than the sum of the parts. You have related this paradox to mathematics with the metaphor "God is a definite integral." Now this is certainly meaningless to anyone who has not learned calculus, and even to those who know calculus its meaning is probably not self-evident. Could you briefly explain the definite integral and in what sense it is God?
Sarah: Briefly? You jest, Tom!
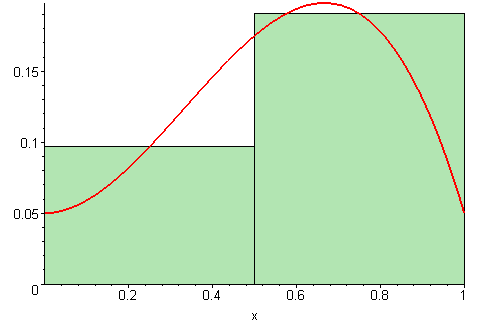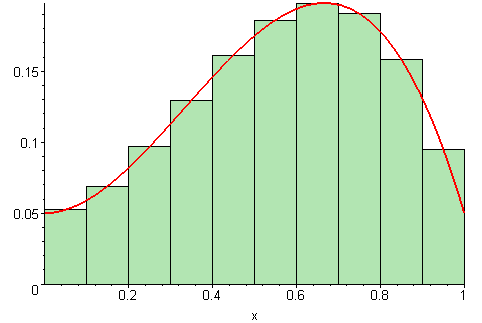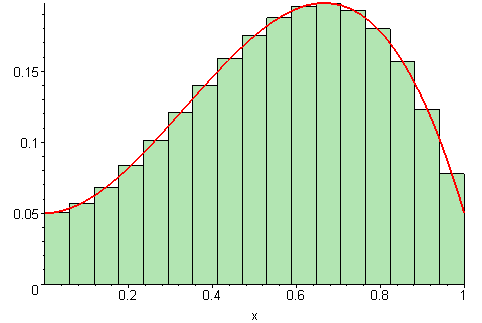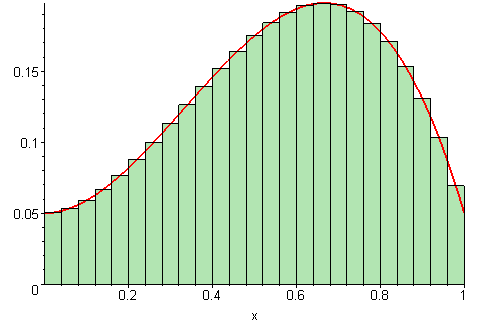
All right, I'll do my best. In its simplest form, the definite integral of calculus is a complex, sophisticated process of adding up many, many geometric areas—so many different areas that there is no end to them. Imagine a stack of paper of various sizes and shapes which is so high it disappears from sight. Some of these sheets of paper are like the ones you put in your computer printer, the ones which are about 8 by 11 inches, or (roughly) 88 square inches in area. Others may be the size of, say, a 3 by 5 inch postcard, or roughly 15 square inches in area. Your task is to add all of them up and come up with the exact number of square inches in the whole bunch. You don't even know how many areas you're adding together, because this is a never-ending process and there are always more. An infinity of areas. Summing up all these areas of this never-ending column of paper is surely impossible, but—and this is a huge "but"—a special mathematical technique called the definite integral allows you to transcend this problem and discover the total sum—the whole column, even though you can't see it. That's not exactly the way the concept is presented in a calculus text, but it's roughly the idea. What this process taught me is how the one and the many are the same.
Mystics like to talk about the unity of everything. There are lots of ways of saying this. Sometimes I think of how many different souls there are in the reality I am experiencing, and how different they all seem to be one from the other. Yet when you add them all up, you just get God.
Tom: In the modern world we are faced more than ever with the confluence of different cultures and religions. It is challenging for many people to understand how these different religions, which appear to be mutually exclusive, can be reconciled. You suggest that Cantor's mathematics of infinity can help to understand the relationship between religions. Could you elaborate on this metaphor and explain a bit about the mathematics of the infinite and how it can help provide a useful understanding of the relationship between religions?
Sarah: You'd probably like this in half a page or less, right? I'm afraid, Tom, that I'm going to cop out here and refer those who are interested to the 35-page chapter called "God the Definite Integral and Cantorian Religion" which appears toward the end of What Number Is God? The metaphor about God as a definite integral dealt with ultimate reality—how everything is related to everything else. The metaphor about Cantorian religion was not so much about ultimate reality as it was about the different kinds of religions which try to deal with that ultimate reality. Some people think, for example, that, while there are many approaches to the "top of the spiritual mountain," there is only one "right" one—that only one will actually get you there. Others think there are several possible routes which will get you to the top, but they "prefer" one over all the others, and that one is their religion of choice. In modern times, greater ease of travel and better communication technologies have increased the world's awareness of this religious pluralism. I suggest in this last chapter of What Number Is God? that a totally new kind of religion is emerging, one that is made up of the set of all these religions. This is not a "better" religion than the others. It is just a different kind of religion. It is structurally different from the others in the same sense that the mathematician Georg Cantor's "set of all sets" was structurally different from all the rest of the other sets. At the same time, this new, highly pluralistic religion that is emerging is also just another religion, subject to all the problems and limitations that any other religion might encounter.
For those who are interested in knowing more about how this structural difference impacts this emerging religion, I refer you to "Matheology and Cantorian Religion," an article I wrote for the Journal of Religious Humanism (Winter/Spring 2004). In this essay I identify seven specific ideas about mathematics which, thanks to Cantor's legacy, are now known to be true, and also seven ways in which these mathematical ideas can be adapted to our spiritual lives. As one example, I write in this article that the "structure of this Cantorian religion lends itself to the acceptance of religious contradictions and paradox. One such paradox is that a Cantorian God both is and is not an infinite God."
Tom: The metaphors discussed above seem to have primary relevance for the abstract understanding of God and the relationships between religion. How can we apply the metaphors in our personal religious lives? Can these metaphors help transform us from self-centeredness to Reality-centeredness? If so, how? Can you share any examples from your life?
Sarah: Excellent questions! I guess if I were to write The Math Mystic's Guide to Creative Spiritual Living, it would probably contain a large section on how behavior and belief inform each other. If the "many" truly believe that they are "one," then, barring duress or other interference, the many are likely to relate together with ease, tolerance, acceptance, and the almost automatic expectation of working for the good of the whole, much as a person's two separate hands naturally work together to benefit the larger body. Similarly, when I act as though I am related to everyone else, I come to believe that I truly am related to everyone else. If I act as though I love my enemy, over time I am likely to do so. I tend to think that anything that helps to demonstrate how we are all related to each other is a spiritual asset. Personally, I have found fertile ground in mathematics for demonstrating many such concepts.
If, however, "duress and other interference" inhibits this otherwise natural progression from "self-centeredness to Reality-centeredness," then I'd pull out the second section of the Math Mystic's Guide—the part about "moral" math. This is the section that culls from the math literature all the possible ways in which mathematics offers insight into conflict resolution, fairness, equity, and so on.
Tom: In What Number Is God? you write that "It is the responsibility of the liberal religious leader to promote such exploration [between mathematics and metaphysics]." What are some of the ways (in addition to your book, of course) that you have done this?
Sarah: I think I've largely addressed these ways in my earlier comments, but I'd like to share with you one of the most meaningful experiences I've had in my attempt to promote exploration between math and metaphysics.
It was 2005 and I had prepared a presentation on moral math as a tiny part of a three-day UNESCO event in Seattle. My "track" was on trustworthiness and justice, and, right before I presented, a middle-aged gentleman shared his personal story about the terrible difficulty he'd had growing up Jewish in Austria after World War II. Another man in our group was also from Austria, and his family had been part of the resistance movement. This second man suggested that the first person's story was one-sided, and the conversation took off from there, with the result that very raw emotions were ignited and even one of the facilitators was choking back tears. Being unable to bring resolution to the situation, the facilitators finally decided just to move forward with the agenda, which was fine with me except that the next item on the agenda was my highly-cognitive presentation on moral math. Oh, no, I groaned inwardly. What on earth was I supposed to do next?
Winging it, I told the group a little about my interest in healing and how I found mathematics a fruitful place to glean fresh, out-of-the-box ideas. Then I led them through an experiential exercise called the dollar auction which I'd found in the literature on mathematical game theory and, after that, through a net-theory exercise which I'd developed to illustrate the way self-organization can emerge from the apparent randomness of chaos theory. To my surprise, I not only conveyed how math might work to promote trust, but I also showed them that it did. As one observer put it, genuine healing took place in the room.
Even the Jewish presenter told me later that he'd found my presentation powerful and personally healing, particularly the part which dealt with the random nature of self-organized emergence, which he related to the situation of the Holocaust. His feelings were echoed in various ways by other participants so that, all in all, it was extraordinarily exciting for me. I had assumed that my work could lead to healing, but this time I actually saw it happen. God's grace that I could experience, even once, such a wonderful affirmation of my work.
Tom: Since writing your book What Number is God? in what ways have your thoughts on this topic developed? In what ways have others developed these kinds of ideas?
Sarah: I have definitely moved more in the direction of action. Now retired, I recently trained to be a mediator in what is known as "interest-based mediation." This is a fabulous process, geared toward having the dissenting parties make their own decision about how to resolve their differences. In the last few years I've taken something of a sabbatical from my own active work on math and religion—no workshops, no lectures, no research of any sort. Still, the possibilities of moral math seem to be calling me, so when I underwent mediation training, I did so with the sense that this new work would at least be compatible with my former work on moral math. To my great excitement I discovered that the mediation centers with which I am affiliated had recently offered a continuing education program that involved chaos theorists from a nearby university. They were demonstrating the very kinds of things I've been preaching about all my ministry.
When I first began studying the relationship between math and spirituality, it was hard to find other people who were involved in the area. In the twenty-plus years since then, that has changed dramatically. Mining mathematics for spiritual inspiration has become a much more recognized and better understood practice.
Tom: You have written that "a renewal of this divine aspect of mathematics will contribute to the overall spiritual health of our contemporary religious institutions" [p.161] and that "Our wider social community stands now at the edge of a new way of thinking, of a paradigm shift." [p.160] Moreover, you have proposed that "The root of renewal lies in our willingness to embrace mathematics as a metaphorical language." [p.162] How do you envision this unfolding in the future? How would you like to see it unfold?
Sarah: Like a hope-flower blooming.
Tom: That's a beautiful image. Would you venture to envision some features of this flower when it has bloomed? How would you hope it might contribute to or change the way people think and act and live?
Sarah: Thanks. Your questions here bring out the Platonic idealist in me. I don't know that we will ever achieve universal peace, serenity, fairness, equity, altruism, unconditional love, and so forth, but I contend that it is worth striving for these things. Life without this intent is of dubious value. Moreover, mathematics is a wonderful mind-opener, as in "thinking outside the box." Where else (besides through a "mystic moment") can we find the tools to help us envision, say, a 4th or 5th or n-th dimensional existence? Mathematicians (especially those interested in string theory) seem to do this with (relative) ease and sometimes they can even translate what these tools lead them to see so that those of us still inside Plato's cave can get at least a partial glimpse of their vision. Of course, it is possible that a hope-flower in full bloom (where conflict and controversy always manifest respect and loving care) would be boring beyond bearing, but that's a risk I'm willing to seed.
Tom: Thank you for taking the time for this interview! I hope that this will be of benefit to people and help bring about the changes you envision.
Sarah: Thank you, Tom, for offering me the opportunity to let more people know of this work. I'd like to emphasize that mathematics is certainly not the only language with which to speak the mystical word. Poetry is another. I've tried this language as well and, if it's okay with you, I'd like to close with a "mathaphorical" poem which I included at the beginning of my "autopoietic" autobiography.
The Strange Attractor of Hope
Takes twenty-eight days minimum,
I'm told, to change neuronal pathwaysfrom ones committed to negativity
to those that prefer positive messages.Fine. I can deal with a February's worth
of hard alteration even if the outcomeis uncertain since calcified power to see
the world through depression's filteris unlikely to skulk away, rebuked
by a simple twist in desire. Still,I shall venture forth like a puppy
testing the ground rules of survivalin this newly reconstructed mind-set
I'm learning to call home.
